해당 내용은 https://bskyvision.com/21 블로그 포스팅 내용이지만 시험기간 때 공부하려고 그대로 퍼왔습니다
문제가 있을시 바로 삭제하겠습니둥
SIFT (Scale-Invariant Feature Transform)은 이미지의 크기와 회전에 불변하는 특징을 추출하는 알고리즘입니다. 서로 다른 두 이미지에서 SIFT 특징을 각각 추출한 다음에 서로 가장 비슷한 특징끼리 매칭해주면 두 이미지에서 대응되는 부분을 찾을 수 있다는 것이 기본 원리입니다. 즉, 그림 1과 같이 크기와 회전은 다르지만 일치하는 내용을 갖고 이미지에서 동일한 물체를 찾아서 매칭해줄 수 있는 알고리즘입니다.

위에 두 이미지에서 동일한 부분인 책을 찾아서 매칭해준 것을 확인할 수 있습니다. 중요한 것은 이미지의 크기도 다르고, 책의 회전? 방향도 다르고, 다른 물체들에 조금씩 가려져 있는데도 일치되는 부분을 잘 찾아서 매칭해주었습니다. 이것이 바로 SIFT의 장점입니다. SIFT는 크기나 회전에 불변하는 특징을 찾아내줍니다. 위의 이미지들은 흑백이라 조금 보기 안 이쁘니 다른 예를 하나 더 살펴보겠습니다. 그림 2와 그림 3을 보시죠 (참고로 이 사진은 부산에 아는 형 결혼식 갔다가 찍은 사진입니다.) 그림 2에서는 왼쪽 아래에 있는 빨간 색 차를 매칭해봤습니다. 차 사진이 회전되었고, 좀 더 흐려졌음에도 잘 매칭되었음을 확인할 수 있습니다.

그림 3에서는 표지판을 매칭했는데, 두 포인트 정도 완전히 엇나간 것을 제외하고는 비교적 잘 매칭되었습니다.

이런 식으로 작동하는 SIFT는 파노라마 영상을 만들 때도 사용됩니다. 파노라마 사진 만드는 알고리즘을 보진 않았지만 아마도 여러 장 조금 겹치게 찍은 사진에서 서로 겹치는 부분을 찾아서 옆에 붙이고 붙여주는 원리를 갖고 있지 않을까 싶네요. 그리고 SIFT는 두 장의 이미지가 좌우로 조금 다른 수평 디스패리티를 갖고 있는 스테레오 이미지를 매칭할 때도 사용될 수 있습니다.
그렇다면, 도대체 SIFT 알고리즘은 어떤 순서를 갖고 있기에 회전과 크기 변화에도 robust하게 서로 매칭되는 부분을 잘 찾아낼 수 있는 것일까요? 절차를 하나씩 잘 살펴보겠습니다. 대략적으로 아래와 같은 순서로 진행됩니다.
1. "Scale space" 만들기
2. Difference of Gaussian (DoG) 연산
3. keypoint들 찾기
4. 나쁜 Keypoint들 제거하기
5. keypoint들에 방향 할당해주기
6. 최종적으로 SIFT 특징들 산출하기
자, 그러면 하나씩 살펴보도록 하겠습니다.
1. "Scale space" 만들기
첫번째로 "Scale space" 만들기입니다. Scale space에 대한 개념은 아래 링크를 참고하세요.(http://bskyvision.com/144) 먼저 원본 이미지를 두 배로 크게 만든 다음에 점진적으로 블러되게 만듭니다. 그리고 원본 이미지를 점진적으로 블러되게 만듭니다. 그 다음에는 원본 이미지를 반으로 축소시킨 이미지에서 또한 점진적으로 블러된 이미지들을 만들어냅니다. 그리고 또 반으로 축소시킨 다음에 점진적으로 블러된 이미지들을 만들어냅니다. (원본 이미지를 일단 2배로 키우는 이유는 나중에 Difference of Gaussian (DoG) 이미지를 만들 때 같은 옥타브 내에서 인접한 2개의 블러 이미지를 활용해서 만들고, 또 그렇게 생성된 DoG 이미지들 중에서 인접한 세 개의 DoG 이미지를 활용해서 Keypoint들을 찾기 때문입니다.) 그림 4에 구현한 결과를 나타냈습니다.

그림 4. Scale space 만든 결과
blurring, 즉 흐리게 만드는 것은 가우시안 연산자와 이미지를 컨볼루션 연산해줌으로 가능합니다. 공식으로 나타내면 아래와 같습니다.
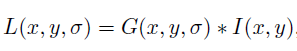
...(1)
여기서 L은 블러된 이미지이고, G는 가우시안 필터이고, I는 이미지입니다. x, y는 이미지 픽셀의 좌표값이고,
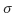
는 "scale" 파라미터입니다. 이거 이름을 왜 scale 파라미터라고 했는지는 잘 모르겠지만, 아무튼 블러의 정도를 결정짓는 파라미터입니다. 값이 클수록 더 흐려집니다. 아래는 가우시안 필터의 공식입니다.

...(2)
점차적으로 블러된 이미지를 얻기 위해서

값을 k배씩 높여갔습니다. 처음

값을
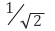
으로, k 는

로 설정했습니다. 2배로 키운 원본이미지가 처음에는

의 값으로 블러되었다면, 그 다음에는 1이 되고, 그 다음에는

, 또 그 다음에는 2의 값으로 블러가 되는 방식입니다. 점점 더 흐려진 결과를 볼 수 있습니다. 원본 이미지에서는

에서 시작해서 k배씩 점차적으로 블러되게 해줍니다. 그리고 원본 이미지의 크기를 가로, 세로 각각 반씩 줄인 다음에는

에서 시작해서 k배씩 점차적으로 블러되게 해줍니다. 같은 사이즈를 갖지만 다른 블러의 정도를 갖는 이미지가 각각 5장씩 존재하고, 총 4개의 그룹을 형성하게 됩니다. 여기서 같은 사이즈의 이미지들의 그룹을 octave라고 명칭합니다. 즉, 세로로 배열되어 있는 이미지들이 한 옥타브를 형성합니다. 아마도 우리가 어떤 물체를 볼 때 거리에 따라 명확하거나 흐리게 보이기도 하고, 크거나 작게 보이기도 하는 현상을 담으려고 이런 방법을 쓰는 것이 아닐까 싶습니다. 이 과정 덕분에 SIFT 특징은 이미지의 크기에 불변하는 특성을 갖게 됩니다.
2. DoG 연산
전 단계에서 저희는 이미지의 scale space를 만들었습니다. 다양한 scale값으로 Gaussian 연산처리된 4 그룹의 옥타브, 총 20장의 이미지를 얻었습니다. 이제 Laplacian of Gaussian (LoG)를 사용하면 이미지 내에서 흥미로운 점들, 즉 keypoint들을 찾을 수 있습니다. LoG 연산자의 작동 원리를 간단히 말하자면, 먼저 이미지를 살짝 블러한 다음에 2차 미분을 계산합니다. 식으로 나타내면 다음과 같습니다.

...(3)
LoG 연산을 통해서 이미지 내에 있는 엣지들과 코너들이 두드러지게 됩니다. 이러한 엣지들과 코너들은 keypoint들을 찾는데 큰 도움을 줍니다. 하지만 LoG는 많은 연산을 요구하기 때문에, 비교적 간단하면서도 비슷한 성능을 낼 수 있는 Difference of Gaussian (DoG)로 대체합니다. LoG, DoG 모두 이미지에서 엣지 정보, 코너 정보를 도출할 때 널리 사용되는 방법들입니다. DoG는 매우 간단합니다. 전 단계에서 얻은 같은 옥타브 내에서 인접한 두 개의 블러 이미지들끼리 빼주면 됩니다. 그림 5는 그 과정을 설명해줍니다.

이 과정을 실제 이미지로 구현한 결과는 그림 6에 있습니다.
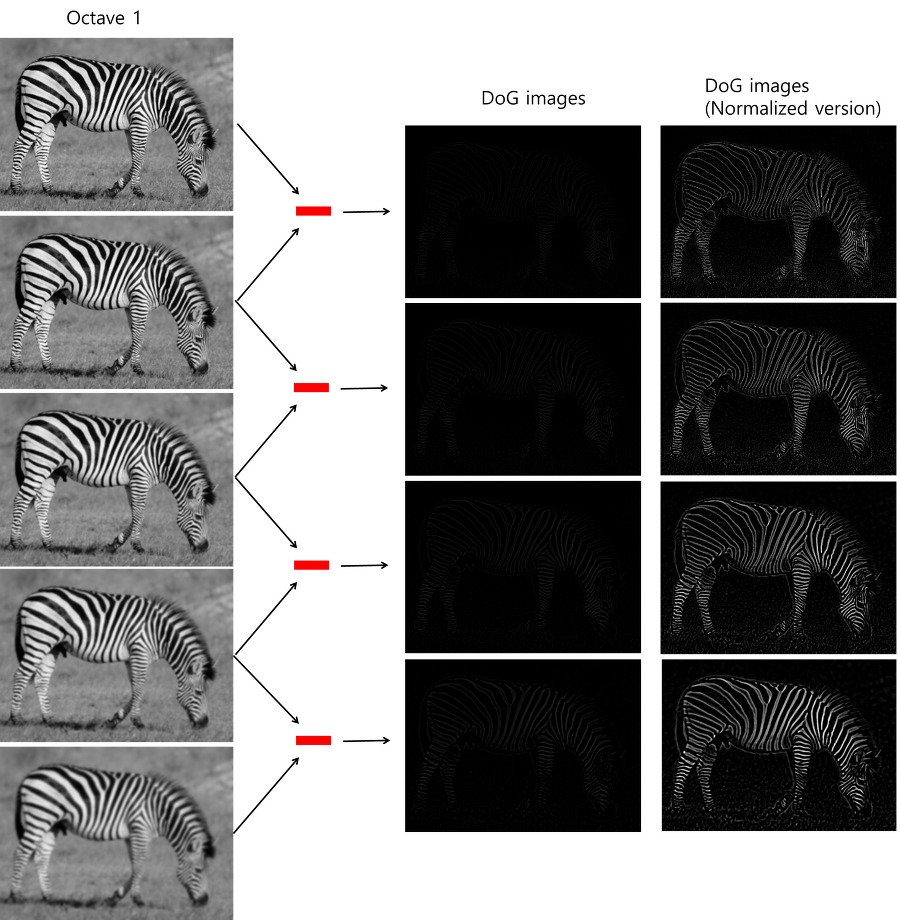
중간에 있는 DoG 이미지들 그냥 검은색 이미지 아닙니다. 컴퓨터 화면이 얼룩진건가 하시는 분들도 있을 텐데 자세히 봐보세요. 얼룩말의 형상이 보일 것입니다. 그래도 잘 안보이는 것 같아서, 정규화한 버전의 DoG 이미지들도 오른쪽에 추가했습니다. 이미지의 엣지 정보들이 잘 도출된 것을 확인할 수 있습니다. 이 과정이 모든 octave에서 동일하게 진행됩니다. 그러면 결과적으로 4개씩, 16장의 DoG이미지를 얻겠죠??
여기서 잠깐 LoG와 DoG에 대해 좀 더 깊이 살펴보고 지나가겠습니다. LoG를 DoG로 대체할 때 시간이 적게 걸린다는 것 외에도 장점이 더 있습니다. LoG는 scale 불변성을 위해
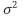
로 라플라시안 연산자를 정규화(normalization)해줘야합니다. 즉, LoG연산자가 아래와 같이 scale-normalized LoG로 변합니다.

...(4)
scale-normalized LoG의 극대값, 극소값은 매우 안정적으로 이미지 특징을 나타냅니다. 그래서 이 극대값, 극소값들은 keypoint의 후보가 되는 것입니다. 그러면 도대체 어떻게 LoG가 DoG로 대체될 수 있을까요? 이것을 증명하기 위해서 열 확산 방정식이 응용됩니다.

...(5)
열 확산 방정식에 의해 이런 관계가 형성된다고 합니다. Gaussian을

에 대해 미분한 것은 LoG에
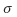
를 곱한 것과 같다는 의미죠. 이것은 미분함수의 성질을 이용하면 다음과 같이 전개될 수 있습니다.

...(6)
양변에 우변의 분모를 각각 곱해주면, 아래와 같은 식이 나오게 되죠.

...(7)
결국 다른 scale을 갖고 있는 Gaussian 이미지들끼리의 합, 즉 DoG는 scale-normalized LoG에 (k-1)을 곱한 것과 거의 같습니다. 따라서 DoG는 scale 불변성을 보장하는

scale 정규화 과정을 자연스럽게 포함하게 됩니다. 그리고 곱해진 (k-1)은 극대값, 극소값을 찾는데는 아무런 영향을 주지 않기 때문에 무시해도 괜찮습니다. 암튼 이러한 방식으로 LoG는 DoG로 무리없이 잘 대체됩니다. (오히려 상당부분 이득을 보면서 대체됩니다.)
이제 이 DoG 이미지들을 활용해서 흥미있는 keypoint들을 찾아낼 것입니다.
3. keypoint들 찾기
이제 DoG 이미지들에서 keypoint들을 찾을 차례입니다. 먼저 DoG 이미지들 내에서 극대값, 극소값들의 대략적인 위치를 찾습니다. 그림 7에 극대값, 극소값의 위치를 찾는 방법이 설명되어 있습니다.
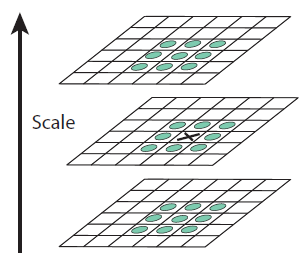
한 픽셀에서의 극대값, 극소값을 결정할 때는 동일한 octave내의 세 장의 DoG 이미지가 필요합니다. 체크할 DoG이미지와 scale이 한 단계씩 크고 작은 DoG 이미지들이 필요합니다. 지금 체크할 픽셀 주변의 8개 픽셀과, scale이 한단계씩 다른 위 아래 두 DoG 이미지에서 체크하려고 하는 픽셀과 가까운 9개씩, 총 26개를 검사합니다. 만약 지금 체크하는 픽셀의 값이 26개의 이웃 픽셀값 중에 가장 작거나 가장 클 때 keypoint로 인정이 됩니다. 그러므로 4장의 DoG 이미지들 중에서 가장 위에 있고 가장 아래에 있는 DoG 이미지들에서는 극대값, 극소값을 찾을 수 없습니다. 이런 방식으로 DoG 이미지의 모든 픽셀에서 Keypoint들을 찾습니다. 좀 더 확실한 이해를 위해 이 과정을 실제 이미지로 구현해보겠습니다. 이번에도 octave1에서의 결과만 보이도록 하겠습니다. 그림 8을 확인하세요. 나머지 octave들에서도 동일한 연산이 이루어진다는 것을 잊지 마세요.

흰색 점들로 표현된 곳이 극대값, 극소값들입니다. 역시 잘 안보이지만 모니터의 각도를 좀 바꿔보면 잘 보이는 각도가 있을거에요. 암튼 이 점들이 일차적으로 keypoint들이 됩니다. 여기서 보면 두 장의 극값 이미지를 얻기 위해서는 4장의 DoG이미지가 필요하다는 것을 알 수 있습니다. 이를 위해서 scale space를 만들 때 5 단계의 가우시안 블러 이미지를 만든 것입니다. 5장의 블러 이미지에서 4장의 DoG 이미지가 나오고, 또 4장의 DoG 이미지에서 2장의 극값 이미지가 나오는 거죠. 네 그룹의 octave를 갖고 있으니, 8장의 극값 이미지를 얻게 됩니다. 그런데, 이렇게 얻은 극값들은 대략적인 것입니다. 왜냐하면, 그림 9에 설명한 것과 같이 진짜 극소값, 극대값들은 픽셀들 사이의 공간에 위치할 가능성이 많기 때문이죠.

그림 9. 진짜 극값의 위치
그런데 우리는 이 진짜 극소값, 극대값들의 위치에 접근할 수 없습니다. 그래서 subpixel 위치를 수학적으로 찾아내야 합니다. subpixel은 이렇게 픽셀들 사이에 위치한 것을 의미하는 것 같습니다. 좀 더 정확한 극값들을 어떻게 찾아내는가 하면, 바로 테일러 2차 전개를 사용합니다. (여기 테일러 전개에 대한 이론적인 내용은 저도 잘 모르겠네요. 일단 대략적인 개념만 이해하고 넘어가셔도 좋습니다.)

...(8)
여기서 D는 DoG이미지이고, x는

입니다. 이걸 x로 미분해서 0이 되게 하는 x의 값, 즉

이 극값의 위치가 됩니다. 계산하면 아래와 같이 구해진다고 합니다.
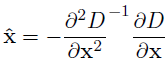
...(9)
이 과정은 알고리즘이 좀 더 안정적인 성능을 낼 수 있게 도와줍니다.
4. 나쁜 Keypoint들 제거하기
이제 전 단계에서 극값들로 찾은 keypoint들 중에서 활용가치가 떨어지는 것들은 제거해줘야 합니다. 두 가지 기준으로 제거해주는데요, 첫번째는 낮은 콘트라스트를 갖고 있는 것들을 제거해줍니다. 그 다음 엣지 위에 존재하는 것들을 제거해줍니다.
먼저 낮은 콘트라스트의 keypoint들을 제거해주는 과정을 살펴보겠습니다. 간단히 DoG 이미지에서 keypoint들의 픽셀의 값이 특정 값(threshold)보다 작으면 제거해줍니다. 저희는 지금 subpixel 위치에서 keypoint들을 갖고 있기 때문에 이번에도 역시 테일러 전개를 활용해서 subpixel 위치에서의 픽셀값을 구합니다. 간단히 위에서 구한

을 (8)에 대입해주면 됩니다. 그 결과는 (10)과 같습니다.

...(10)
이 값의 절대값이 특정 값보다 작으면 그 위치는 keypoint에서 제외됩니다.
이제 두번째로 엣지 위에 존재하는 keypoint들을 제거해줍니다. 그 이유를 저는 다음과 같이 이해했습니다. DoG가 엣지를 찾아낼 때 매우 민감하게 찾아내기 때문에, 약간의 노이즈에도 반응할 수 있는 위험이 있습니다. 즉, 노이즈를 엣지로 찾아낼 수도 있다는 것입니다. 그래서 엣지 위에 있는 극값들을 keypoint로 사용하기에는 조금 위험성이 따릅니다. 따라서 좀 더 확실하고 안전한 코너점들만 keypoint로 남겨주는 것이죠. 이를 위해서 keypoint에서 수직, 수평 그레디언트를 계산해줍니다. 수평 방향으로는 픽셀 값이 어떻게 변화하는지, 수직 방향으로는 픽셀 값이 어떻게 변화하는지 변화량을 계산하는 것입니다. 만약 양 방향으로 변화가 거의 없다면 평탄한 지역(flat region)이라고 생각할 수 있습니다. 근데 수직 방향(or 수평 방향)으로는 변화가 큰데, 수평 방향(or 수직 방향)으로는 변화가 적으면 엣지(가장자리)라고 판단할 수 있습니다. 또 수직, 수평 방향 모두 변화가 크면 코너(모서리)라고 판단할 수 있구요. 설명이 부족하다면, 아래 그림10을 보세요.

이 중에서 코너들이 좋은 keypoint들입니다. 따라서 우리의 목적은 코너에 위치한 keypoint들만 남기는 것입니다. Hessian Matrix를 활용하면 코너인지 아닌지 판별할 수 있다고 합니다. 이 두 제거 과정을 통해 그림 11에서 확인할 수 있듯이 keypoint의 갯수는 상당히 줄어듭니다. 흰 점들이 상당히 많이 줄어들었죠.

이제는 이 keypoint들에게 방향을 할당해줄 차례입니다.
5. keypoint들에 방향 할당해주기
전 단계에서 우리는 적당한 keypoint들을 찾았습니다. 이 keypoint들은 scale invariance(스케일 불변성)를 만족시킵니다. 이제는 keypoint들에 방향을 할당해줘서 rotation invariance(회전 불변성)를 갖게 하려고 합니다. 방법은 각 keypoint 주변의 그레디언트 방향과 크기를 모으는 것입니다. 그런 다음 가장 두드러지는 방향을 찾아내어 keypoint의 방향으로 할당해줍니다. 그림 12와 같이 하나의 keypoint 주변에 윈도우를 만들어준 다음 가우시안 블러링을 해줍니다. 이 keypoint의 scale값(블러의 정도를 결정해주는 파라미터)으로 가우시안 블러링을 해줍니다.

그 다음에 그 안에 있는 모든 픽셀들의 그레디언트 방향과 크기를 다음의 공식들을 이용해서 구합니다.

...(11)
그 결과는 그림 13과 같습니다.

여기서 그레디언트 크기에는 가우시안 가중함수를 이용해서 keypoint에 가까울수록 좀 더 큰 값을, 멀수록 좀 더 작은 값을 갖게 해줍니다. 이 과정은 그림 14에 있습니다.

이제 각 keypoint에 어떻게 방향을 할당해주는지 살펴보도록 하겠습니다. 먼저 36개의 bin을 가진 히스토그램을 만듭니다. 360도의 방향을 0~9도, 10~19도, ... , 350~359도로 10도씩 36개로 쪼갭니다. 그래서 만약 28도면 3번째 bin을 그레디언트 크기만큼 채우는 것입니다. 여기서 그레디언트 크기는 가중처리된 값입니다. 윈도우 내의 모든 픽셀에서 그레디언트 방향의 값을 이런 식으로 해당하는 bin에 채워줍니다. 그러면 그레디언트 방향에 대한 히스토그램이 완성됩니다. 그림 15를 보시죠.

이런 히스토그램이 만들어집니다. 가장 높은 bin의 방향이 keypoint의 방향으로 할당됩니다. 또 여기서 만약 가장 높은 bin의 80% 이상의 높이를 갖는 bin이 있다면 그 방향도 keypoint의 방향으로 인정됩니다. 한 keypoint가 두 개의 keypoint로 분리되는 것입니다. 마찬가지로 만약 3개의 bin이 가장 높은 bin의 80% 이상의 높이를 갖는다면 총 4개의 keypoint로 분리됩니다. 이제 keypoint들에 방향을 할당해주는 작업이 완료되었습니다.
6. 최종적으로 SIFT 특징들 산출하기
지금까지 keypoint들을 결정해왔습니다. 우리는 지금 keypoint들의 위치와 스케일과 방향을 알고 있습니다. 그리고 keypoint들은 스케일과 회전 불변성을 갖고 있습니다. 이제 이 keypoint들을 식별하기 위해 지문(fingerprint)과 같은 특별한 정보를 각각 부여해줘야 합니다. 각각의 keypoint의 특징을 128개의 숫자로 표현을 합니다. 이를 위해 keypoint 주변의 모양변화에 대한 경향을 파악합니다. keypoint 주변에 16x16 윈도우를 세팅하는데, 이 윈도우는 작은 16개의 4x4 윈도우로 구성됩니다. 그림 16을 확인하세요.
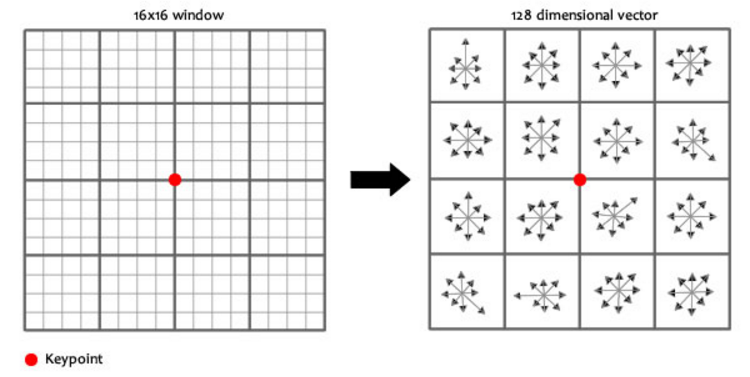
16개의 작은 윈도우에 속한 픽셀들의 그레디언트 크기와 방향을 계산해줍니다. 전 단계에서 했던 것과 비슷하게 히스토그램을 만들어주는데, 이번에는 bin을 8개만 세팅합니다. 360도를 8개로 쪼갤 것입니다. 0~44, 45~89, 90~134, ... , 320~359로 나눠지겠죠? 역시 그레디언트 방향와 크기를 이용해서 bin들을 채웁니다. 결국 16개의 작은 윈도우들 모두 자신만의 히스토그램을 갖게 됩니다. 16개의 작은 윈도우마다 8개의 bin값들이 있으므로, 16 x 8을 해주면 128개의 숫자(feature vector)를 얻게 됩니다. 이것이 바로 keypoint의 지문이 되는 것입니다. 아직 회전 의존성과 밝기 의존성을 해결해야합니다. 128개의 숫자로 구성된 feature vector는 이미지가 회전하면 모든 그레디언트 방향은 변해버립니다. 회전 의존문제를 해결하기 위해 keypoint의 방향을 각각의 그레디언트 방향에서 빼줍니다. 그러면 각각의 그레디언트 방향은 keypoint의 방향에 상대적이게 됩니다. (예를 들어 keypoint의 방향을 구한 것이 20-29도라면 24.5도를 keypoint 주변 16개의 4x4 윈도우의 방향에서 빼주면, 16개의 윈도우의 방향은 keypoint 방향에 상대적이게 됩니다.) 그리고 밝기 의존성을 해결해주기 위해서 정규화를 해줍니다. 이렇게 최종적으로 keypoint들에게 지문(fingerprint)을 할당해줬습니다. 이것이 바로 SIFT 특징입니다.
그렇다면 SIFT로 이미지 매칭을 어떻게 하는 것일까요? 먼저 두 이미지에서 각각 keypoint들을 찾고 지문을 달아줬다면, 이 지문값들의 차이가 가장 작은 곳이 서로 매칭되는 위치인 것입니다.
'ComputerVision' 카테고리의 다른 글
| OpenCV week10(2) Object Tracking - Cam Shift Algorithm (0) | 2021.05.13 |
|---|---|
| OpenCV week10 Object Tracking - MeanShift Algorithm (0) | 2021.05.12 |
| OpenCV_week09 Feature Detection_Shi-Tomasi Corner Detection & Good Featur to Track (0) | 2021.05.03 |
| OpenCV_week09 Feature Detection_Harris Corner Detection (0) | 2021.05.03 |
| OpenCV_week07(DFT, Tamplate Matching) (0) | 2021.04.15 |